Many heated debates have arisen because of this topic but neither side is completely right. First option is clear, for 5 cards you lock your prey and stop thinking about it so let's evaluate second option.

When you click on the 1 card option it will give you a different bonus than what is currently active and reset the 2 hours timer on the bonus. This is true if your bonus is maxed at 10 stars, if it isn't you can still roll the same bonus just with more stars. So let's start with some maths, considering the options as 1 to 4 (Experience, Loot, Damage Boost and Damage Reduction):
- If you have option 1 selected and want to reach option 2, the chances in a single try are 1/3 or 33%.
- If you want to reach option 1 from any other option the chances are again 1/3.
- If you didn't get option 1, the chances will always be 1/3 in every single roll, costing you 1 card each.
It is clear that the minimum we will spend to reach the same option we started with is 2 cards, at a 1/3 chance of success since we don't care what the first roll gave us.
The expected success of this can just be calculated by 1 / (1/3) = 3 / 1 or just 3. If we add the original card, the expected success is in 4 tries. So using the 1 card roll is expected to succeed after 4 tries (from the starting point of view) compared to the 5 cards of the locked prey.
But since we all have unlucky friends, the real distribution of probability is the following:
| Cards spent | Accumulated success |
| 2 | 0.333333 |
| 3 | 0.555556 |
| 4 | 0.703704 |
| 5 | 0.802469 |
| 6 | 0.868313 |
| 7 | 0.912209 |
| 8 | 0.941472 |
| 9 | 0.960982 |
| 10 | 0.982658 |
Despite 4 being the expected number of cards needed, the success rate is "only" 70.37% so if you feel unlucky you can lock your bonus for 5 cards. Statistical probability will catch up in the long run and rolling with 1 card gives better chances.
Bonus consideration with 2 accepted prey bonuses
The above is true for players wanting to just maximize the experience prey bonus or for EKs, who for many hunts need to keep locking defense preys. Many people accept both the Experience and Damage Boost prey bonuses since they both achieve a similar goal.
In this situation the chances of success are:
- 1/3 in the first reroll, since one of the remaining options is already valid.
- 2/3 in any other failed reroll.
The calculation of the expected amount of cards needed is a bit more tricky since the first roll can already provide a valid outcome, but we can reach it with:
Expected cards = 1*1/3 + (1+(1 / (2/3) ))*2/3 = 1/3 + 2.5*2/3 = 2 cards
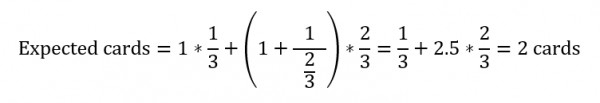
The first 1*1/3 represents the first roll while the second part represents the cards used if we fail. The distribution of probability also reflects this increased chances:
| Cards spent | Accumulated success |
| 1 | 0.333333 |
| 2 | 0.666667 |
| 3 | 0.888889 |
| 4 | 0.962963 |
| 5 | 0.987654 |
| 6 | 0.995885 |
If you still have any existing doubts or would like to challenge my probabilities, please write a comment!
I would also like to take this opportunity to explain another bit about prey bonuses. If you like your selected bonus (because it is 10 stars or whatever) you can lock the bonus by rolling the prey creature using the free / gold option. The next time you select a creature in this prey slot, the bonus will be the same.